К проведению исследования магических квадратов 9-го порядка (9х9) подтолкнул интерес к матричному квадрату из статьи Андрея Рехтина «Еретический взгляд Do Nачала и закон девятки. Часть 3. Математическая магия 369».
«Таблица 9Х9 ниже не случайное множество чисел. Она подчиняется строгой закономерности.
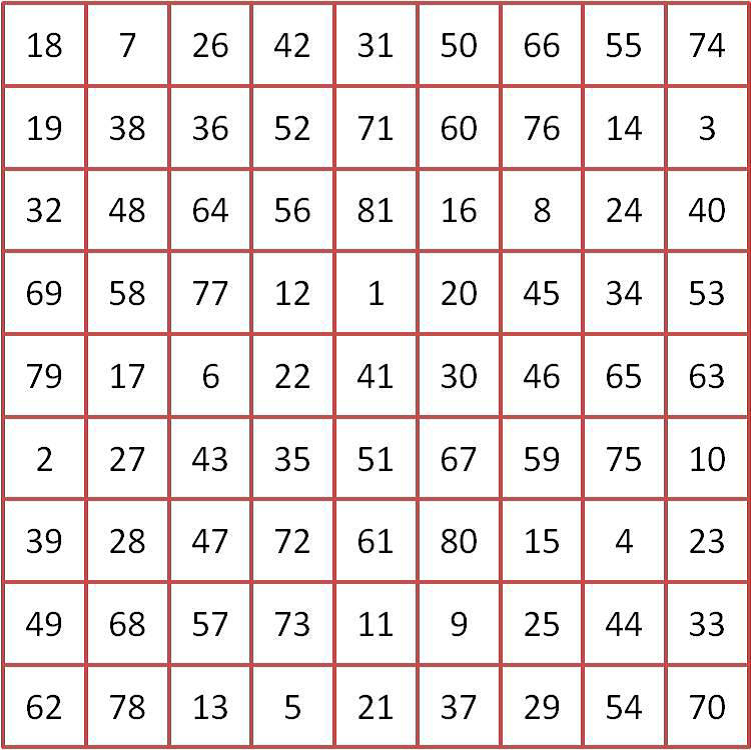
9*(92+1)/2=369.Эта формула есть ни что иное как формула магического квадрата девятого порядка 9. Где, 369 является магической константой такой матрицы. Уникальность матрицы в её удивительной симметрии, где сумма любого столбца, строки или диагонали даёт 369».
Способов построения магического квадрата девятого порядка множество, которых не трудно отыскать в интернете. Целью проведения исследования конечно возобладало любопытство в отношении квадрата «369», но в процессе поиска обнаружились удивительные вещи, о которых не смел предполагать.
Один из предложенных способов предполагает использование цифровых корней из числа. Точнее и правильнее говорить о строительстве квадрата именно с цифровых корней, затем только как следствие возникает магический квадрат. Следует обратить внимание не на способ построения магического квадрата, а на инструменты и технологии при помощи которых создается методика формирования квадрата «369». Инструменты получили название «Конструкт» и «Эннеаграмма». К технологиям следуетотнести возникновение диорамной матрицы. По окончании прилагаются доказательства предложенного способа на готовых образцах магических квадратов, взятых из интернета для исследования. Их можно пропустить и не читать. Это уже для любителей посчитать, потому что считать сложно и скучно, требует усидчивости, внимательности и наличие времени, которого ой как не хватает.
Один из способов формирования матрицы «369».
Есть матрица квадратным размером 9 на 9, состоящая из 81-й пустых ячеек. Задача - вложить числа от 1 до 81 таким образом, чтобы сумма чисел в каждых строчках, столбцах и диагоналях равнялась 369.
В исследовании используется правило формирования цифровых корней из чисел согласно теософскому сложению. Например, число 12 имеет цифровой корень 3 (1+2=3).
Укладываем в таблицу №1 все числа от 1 до 99 в 9 строк и 11 столбцов, 9х11=99. В таблице получается 99 ячеек. В строку расставляем числа, которые имеют цифровой корень начиная с единицы и заканчивая девяткой. Всего девять цифровых корней 1,2,3,4,5,6,7,8,9 и значит девять строчек. Каждый одноименный корень имеют ровно по 11 чисел и значит получаются одиннадцать столбцов.
Таблица №1 «Цифровые корни до 99 из одно- и двузначных чисел»
|
N NN |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
1 |
1 |
10 |
19 |
28 |
37 |
46 |
55 |
64 |
73 |
82 |
91 |
|
2 |
2 |
11 |
20 |
29 |
38 |
47 |
56 |
65 |
74 |
83 |
92 |
|
3 |
3 |
12 |
21 |
30 |
39 |
48 |
57 |
66 |
75 |
84 |
93 |
|
4 |
4 |
13 |
22 |
31 |
40 |
49 |
58 |
67 |
76 |
85 |
94 |
|
5 |
5 |
14 |
23 |
32 |
41 |
50 |
59 |
68 |
77 |
86 |
95 |
|
6 |
6 |
15 |
24 |
33 |
42 |
51 |
60 |
69 |
78 |
87 |
96 |
|
7 |
7 |
16 |
25 |
34 |
43 |
52 |
61 |
70 |
79 |
88 |
97 |
|
8 |
8 |
17 |
26 |
35 |
44 |
53 |
62 |
71 |
80 |
89 |
98 |
|
9 |
9 |
18 |
27 |
36 |
45 |
54 |
63 |
72 |
81 |
90 |
99 |
где N-номера столбцов; NN-цифровой корень.
Таблица состоит из 9 строк и 11 столбцов. Следует обратить внимание на сакральную связку «9-11».
Для заполнения матрицы «9х9» используем числа от 1 до 81, то есть первые девять столбцов.
Таблица №2 «Числа для матрицы 9х9»
|
N NN |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
1 |
10 |
19 |
28 |
37 |
46 |
55 |
64 |
73 |
|
2 |
2 |
11 |
20 |
29 |
38 |
47 |
56 |
65 |
74 |
|
3 |
3 |
12 |
21 |
30 |
39 |
48 |
57 |
66 |
75 |
|
4 |
4 |
13 |
22 |
31 |
40 |
49 |
58 |
67 |
76 |
|
5 |
5 |
14 |
23 |
32 |
41 |
50 |
59 |
68 |
77 |
|
6 |
6 |
15 |
24 |
33 |
42 |
51 |
60 |
69 |
78 |
|
7 |
7 |
16 |
25 |
34 |
43 |
52 |
61 |
70 |
79 |
|
8 |
8 |
17 |
26 |
35 |
44 |
53 |
62 |
71 |
80 |
|
9 |
9 |
18 |
27 |
36 |
45 |
54 |
63 |
72 |
81 |
В дальнейшем таблица №2 будет использоваться каждый раз при составлении индивидуальной матрицы «369».
Сейчас про числа можно забыть, они понадобятся в последнюю очередь, когда сформируется диорама - двусторонняя матрица, состоящая из девяти цифр. Эти девять цифр будут олицетворять цифровые корни. В зале (фото 1) выставлена картина, предусматривающая двусторонний просмотр посетителями художественной галереи. Это и есть разновидность диорамы.

Фото 1.
Для примера что такое цифровая диорама:
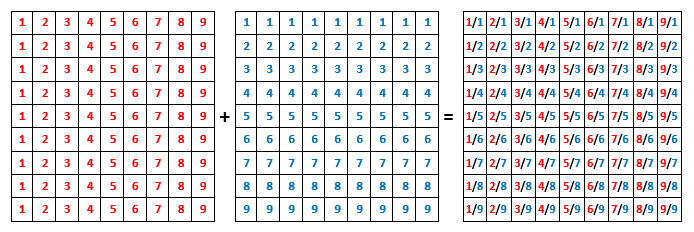
Во сформировавшийся цифровой диораме появилась запись цифр через дробь. Осталось заменить дробную запись в диораме на числа из таблицы №2. И все, вуаля, готова числовая матрица. К примеру 3/8 следует заменить на число из таблицы №2, которое занимает 3-ю строчку и 8-й столбец. Столбцы и строчки можно инвертировать, тогда при 3-м столбце и 8-й строчке будет число 26. При заполнении таблицы «9х9» я в качестве примера буду использовать первый вариант из двух.
Технология формирования дробной записи.
Вспомним матрицу «Русского Всемера» и как она составляется. Сначала в матрице записывается диагональ из чисел, получающихся из золотого числа, последовательно возводимого в положительную степень для формирования возрастающей последовательности чисел в области увеличения мерности числа и последовательно возводимого в отрицательную степень для формирования убывающей последовательности чисел в области уменьшения мерности числа.
Дальше находится коэффициент для столбцов или строк, позволяющий заполнить оставшиеся пустые ячейки относительно числа в диагонали.
В нашем случае технология заполнения матрицы подобна. Сохраняется принцип подобия.
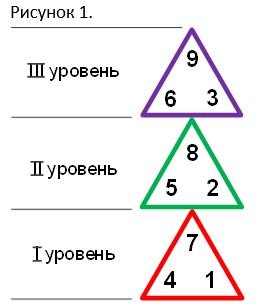
Впору рассказать о цифрах, прежде чем заполнять ими диораму, какое место они занимают по отношению к друг другу и насколько они комбинируют друг с другом. В качестве наглядного пособия возьмем рисунок из статьи «Симметрия чисел», где показана цифровая пирамида, не по форме, по содержанию.
В свою очередь цифровая пирамида сложилась из звезды Инглии с расставленными цифрами.
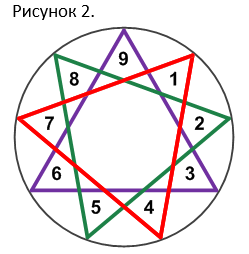
В результате правильной расстановки цифр в диораме формируется диорамный конструкт следующего вида:
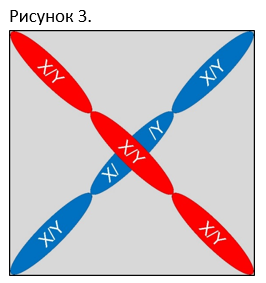
Овалами показана триада цифр. X и Y - это цифровые корни триады цифр. Могут быть - X=3, X=6, X=9, Y=3, Y=6, Y=9 и другие варианты. В записи выглядят так - 3/3, 3/6, 6/6 и так далее. В диагонали, строке и столбце последовательность записи сохраняется.
Итак, составляется диорамная диагональ согласно предложенного конструкта. Дальше для заполнения матричных пустых ячеек вместо коэффициента «Русского Всемера» накладывается эннеаграмма из цифрового ряда на каждую цифру диагонали. После заполнения матричной диорамы заменяется дробная запись числами из таблицы №2.
Для формирования эннеаграмм необходимо:
1) эннеаграмма объединяет все девять цифр, цифры не повторяются;
2) девять цифр разбиваются на тройки при условии, что каждая тройка в сумме даст цифровой корень или 3, или 6, или 9 (возможно другие варианты).
К примеру, для цифрового корня 3 получаются три варианта троек.
Три тройки (1-5-6)-(4-8-9)-(7-2-3)
(1-5-6)→1+5+6=12→1+2=3
(7-2-3)→7+2+3=12→1+2=3
(4-8-9)→4+8+9=21→2+1=3
Три тройки (1-2-9)-(4-5-3)-(7-8-6)
(1-2-9)→1+2+9=12→1+2=3
(4-5-3)→4+5+3=12→1+2=3
(7-8-6)→7+8+6=21→2+1=3
Три тройки (1-8-3)-(4-2-6)-(7-5-9)
(1-8-3)→1+8+3=12→1+2=3
(4-2-6)→4+2+6=12→1+2=3
(7-5-9)→7+5+9=21→2+1=3
По своей сути эннеаграмма это бесконечный ряд цифр определенной последовательности, которая повторяется через девять цифровых знаков.
…123456789123456789123456789123456789123456789123456789…
или
…135792468135792468135792468135792468135792468135792468…
Некоторые спросят: -А где ноль? Он ведь тоже применяется в русском счете. Ноль - круг как раз и нужен, чтобы выделить ряд из девяти цифр от остальных. Ноль можно расставить в любом месте. Бесконечный ряд цифр примет вид:
…1234о567891234о567891234о567891234о567891234о56789…
Тогда ряд цифр можно облечь в круг, расставить их согласно занятым местам и цифровой ряд примет графический рисунок, по контуру которого будет продолжаться бесконечная цифровая цепочка. Это есть эннеаграмма, образное представление цифрового ряда.
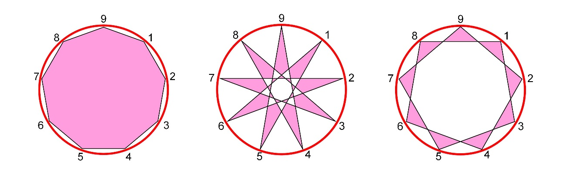
Для составления и демонстрации эннеаграмм применим механизм открывания сейфа. Нужно повернуть несколько колесиков таким образом, что при определенном положении их относительно друг друга происходит разблокирование замка и сейф тогда можно открыть. В нашем случае треугольники (красный 1-4-7, зеленый 2-5-7, фиолетовый 3-6-9) из цифровой пирамиды (рисунок 1) размещаем в центре и каждый размещаем на своих цветных колесиках (рисунок 4).
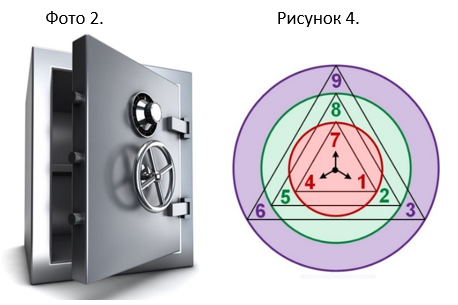
Сейчас будем шифровать, поворачивая зеленое и фиолетовое колесико по- и против часовой стрелки, красное колесико неподвижно. Цель - получить триаду цифр с цифровым корнем или 3, или 6, или 9. Результаты занесем в таблицу №3.
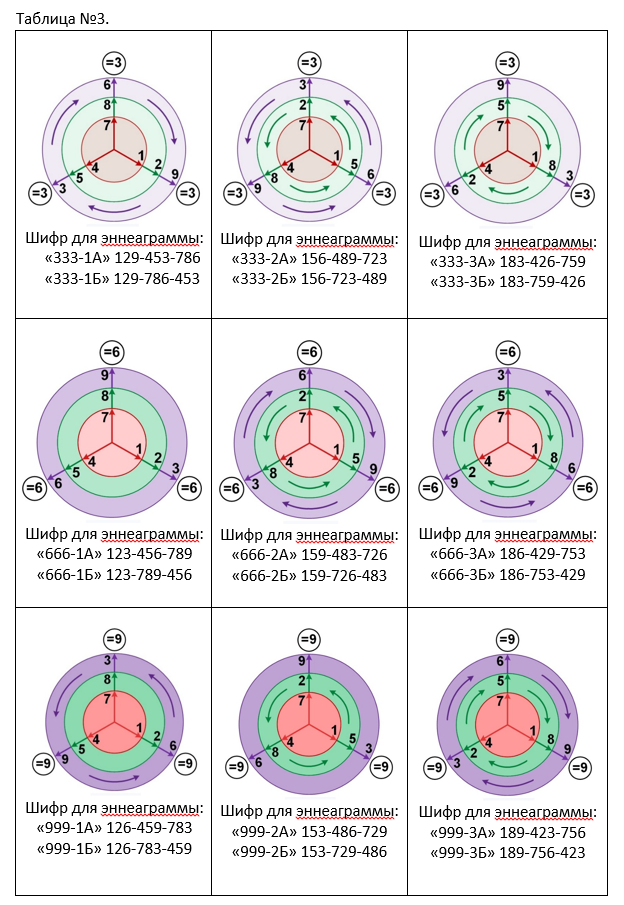
В каждом шифре возникают две цепочки триад цифр в разной последовательности из которых составляется эннеаграмма. В дальнейшем, если в примерах встретится зашифрованная запись эннеаграммы «666-2Б», то подразумевается цепочка цифр 159-726-483. Цепочка имеет бесконечную продолжительность «…-159-726-483 - 159-726-483 - 159-726-483 - 159-726-483-…»
Представим каждую эннеаграмму графическим рисунком и занесем в таблицы №4, №5, №6. Если следовать маршрутом по контуру фигуры эннеаграммы, то начиная с выбранного узла через девять поворотных узлов снова вернемся в начальный узел.
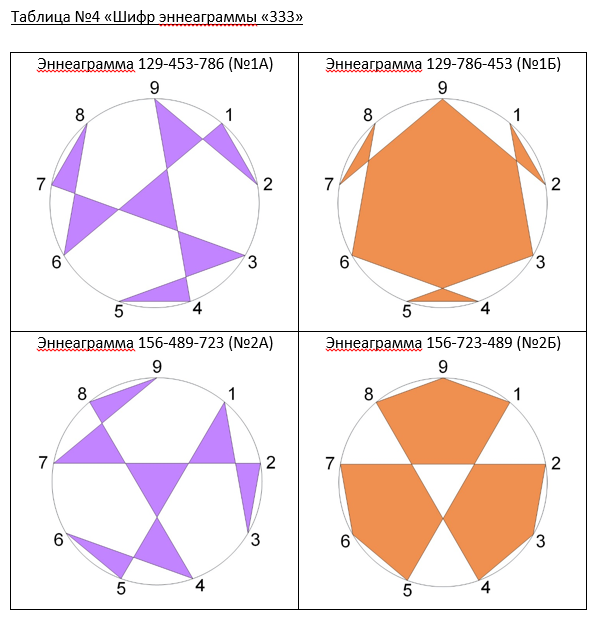
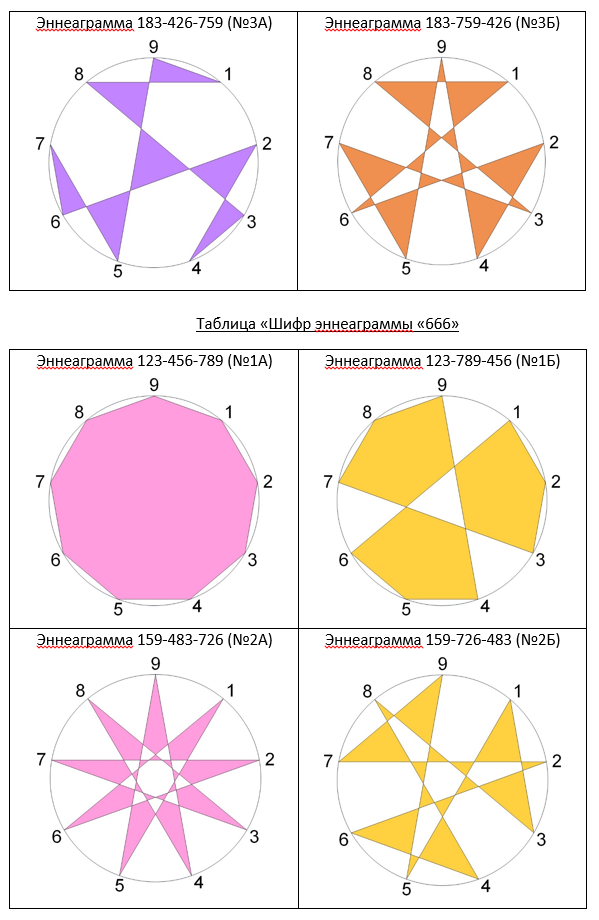
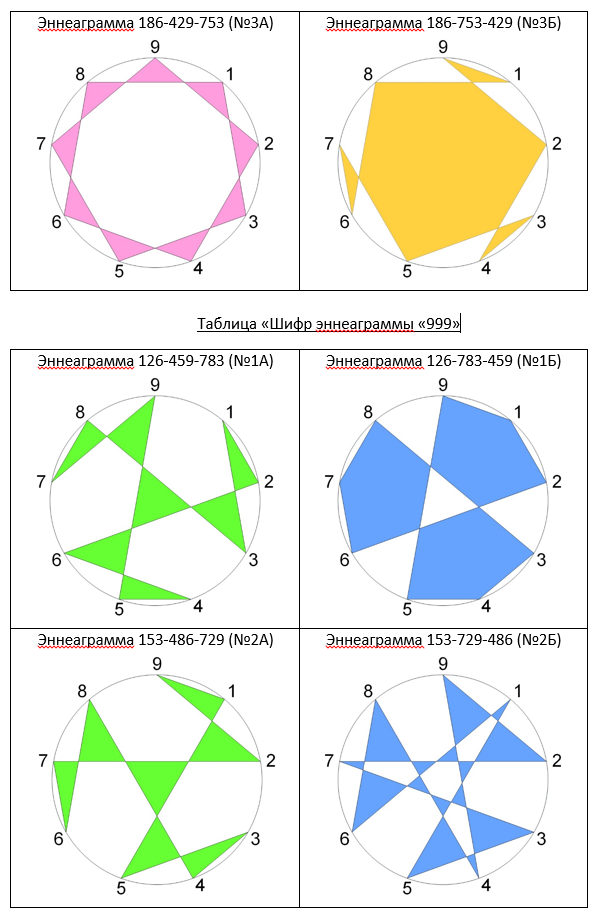
Эннеаграммы очень напоминают детскую игрушку «Калейдоскоп». Здесь плоская проекция эннеаграмм, поэтому и матрица квадратная. Кстати эннеаграмма обличена в круг, а магия чисел 369 обличена в квадрат. Чем вам не иллюстрация решения задачки «Квадратура круга». Продолжу про детскую игрушку «Калейдоскоп». Как дети радуются, когда смотрят в глазок трубы и видят цветной пространственный узор. Как они восхищаются, когда поворачивая трубу, получаются новые искрящиеся, переливающиеся причудливые узоры.
Представьте сейчас незатейливый узор в виде объемной эннеаграммы, тогда должна получиться объемная форма с ячейками, где расставлены числа, образующие магические константы. Это и тетраэдры, и кубы, и додекаэдры и другие более совершенные формы насколько позволяет фантазия.
Особенности графических рисунков:
- в 1-м столбце фиолетовые и зеленые фигуры подобны, имеют семь треугольных элементов. В сказке Валентина Катаева «Цветик-семицветик» говориться о девочке, которой добрая старушка подарила волшебный цветок с семью лепестками желтого, красного, зеленого, синего, оранжевого, фиолетового и голубого цвета. При этом, чтобы исполнилось желание нужно оторвать один лепесток и произнести волшебные слова:
 |
Лети, лети, лепесток,
Через запад на восток,
Через север, через юг,
Возвращайся, сделав круг.
Лишь коснешься ты земли -
Быть по-моему вели. |
Лишь оторвав последний лепесток цветка девочка смогла сотворить настоящее чудо. Так и атомные структуры из которых состоит наш физический плотный мир, в том числе и мы с вами, имеют частоты сопровождения и несущую частоту. «Отрывая» от атомной структуры по частоте сопровождения, атомная структура сохраняет свою конструкцию, но «сорвав» несущую частоту атомная структура рассыпается на первичные материи, исчезает. Надо только придать потоку первичных материй характеристику целеполагания в развитии на основе истины о Сотворенном мире.
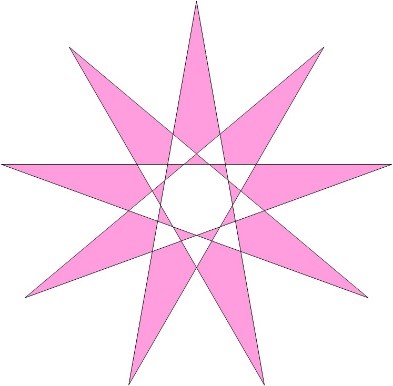
- в 1-м столбце образовались розовые фигуры совершенной симметричной формы. Изумительная красота! Особенно - девятиконечная звезда. В отдельно взятом луче расположились два белых элемента и три поменьше ближе к центру, словно вложенные пирамиды.
Те, кто бывал в Санкт-Петербурге в Исаакиевском соборе видели присутствие розочки в орнаменте центральной части мозаичного пола.
Если выделить часть центрального круга, то из основания этой части выглядывает одна дальнего плана пирамида, две среднего плана пирамиды, три ближнего плана пирамиды. Дальняя и средняя пирамиды одинаковые по высоте, ближняя маленькая по высоте до точки откуда появляется дальняя пирамида. Всего по 18 штук всех трех видов пирамид. Девяти лучевая звезда и восемьнадцатилучевая розочка имеют общий корень девять. По всей видимости в этом месте подземный концентратор обеспечивал энергоинформацией 461-й Генотип Мозга в полном объеме.
- 2-й столбец примечателен тем, что во всех трех таблицах присутствуют три одинаковые фигуры голубого, желтого и оранжевого цветов.
Для рассмотрения выделю их отдельно, потому что они многое что «говорят».
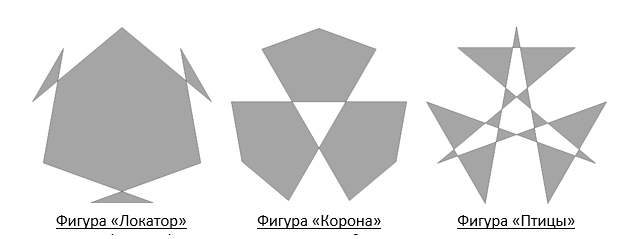
Приведу фотографию Андрея Рехтина «Герб дома Винчи». Частичное видение герба приведено в статье «Герб дома Винчи». Новый оборот прочтения заложенного смысла в гербе приобрело после составления эннеаграмм.

Фигура «Локатор» олицетворяет приемо-передающее устройство. На гербе представлено восьмиконечной звездой «Мальтийский крест».

Фигура «Корона» олицетворяет преобразовательное устройство, позволяющее трансформировать энергоинформацию, дешифровать тексты из эфира и многое другое.

Фигура Птицы» олицетворяет проводниковое устройство, позволяющее целенаправленно переправлять энергоинформацию, своего рода трубки связи по принципу башни Шухова.

На бытовом языке в плане понимания лучше представить сферу энергетики. Выработку электроэнергии производят генерирующие системы (ТЭЦ, ГЭС, ГРЭС, АЭС, солнечные батареи, ветряные «мельницы» и другие). Это все источники питания, которые представляют передающее устройство. Затем электроэнергия передается по проводам ЛЭП или кабелям до потребителя через преобразующие устройства, которые повышают или понижают напряжение с целью уменьшения потери электроэнергии в проводах и кабелях. Преобразование происходит при помощи трансформаторов на подстанциях. Конечной точкой доставки электроэнергии являются потребители (заводы, организации, жилой сектор и другие). Их еще называют техническим термином источники нагрузки. Возникает цепочка: Источник питания-Трансформатор повышающий-Провода ЛЭП-Трансформатор понижающий-Провода ЛЭП-Источник нагрузки. Вся эта триединая система есть комплекс приемо-передающих устройств, преобразующих устройств и транспортирующих устройств.
Дмитрий Харюшин
2019.01.08







